Area-, Power-, and Delay-Optimized 2D FIR Filter Architecture for Image Processing Applications

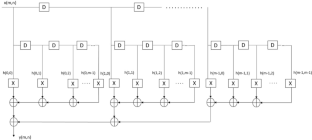
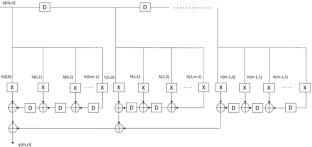
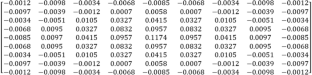
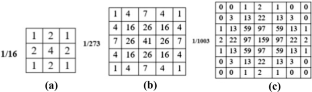
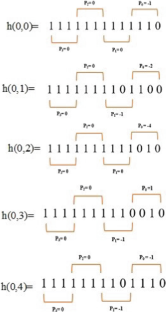
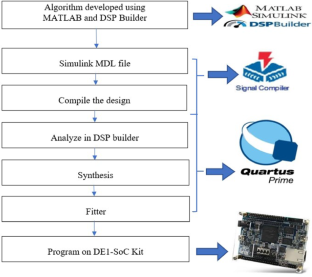
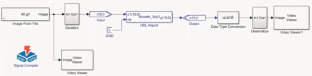
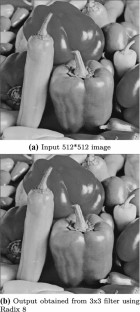
The 2D finite impulse response filters are efficient and are of low complexity, and they are often used for image restoration, image enhancement, and denoising applications. The 2D FIR filter architecture usually includes multipliers implemented using a network of adders/subtractors and shifters, which can be further optimized. Radix-2r multiplication is used for area, power, and delay optimization in the proposed research work. The symmetric 2D FIR filter coefficients considered in the present work are obtained using the modified Park–McClellan transformation method and are optimized using radix-2r multiplication. These coefficients are implemented using fully direct and hybrid II architectures and in gate-level Verilog HDL. The optimized filter’s efficacy is checked using Intel DSP Builder and synthesized using the Cadence RTL compiler. The results of both FPGA and ASIC synthesis results are compared to previous studies. The area, power, and delay results show that the proposed filter occupies less area, consumes less power, and has less delay than existing optimizations. Additionally, this optimization approach is implemented on standard coefficients of \(3 \times 3\) , \(5 \times 5\) , and \(7 \times 7\) kernels. The FPGA results of these kernels are also compared with previous studies.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save
Springer+ Basic
€32.70 /Month
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Buy Now
Price includes VAT (France)
Instant access to the full article PDF.
Rent this article via DeepDyve



Similar content being viewed by others
A Pareto-Optimal Multi-filter Architecture on FPGA for Image Processing Applications
Article 11 March 2019

Efficient Techniques for FIR Filter Designing
Chapter © 2022

Efficient VLSI Architectures of Multimode 2D FIR Filter Bank using Distributed Arithmetic Methodology
Chapter © 2024
Data Availability
Data are available on request due to privacy/ethical restrictions.
References
- A. Benyamina, S. Moulahoum, FPGA in the loop based single phase power factor correction, in 2019 Progress in Applied Electrical Engineering (PAEE) (IEEE, 2019), pp. 1–6
- T. Bindima, E. Elias, Design and implementation of low complexity 2-d variable digital fir filters using single-parameter-tunable 2-d farrow structure. IEEE Trans. Circuits Syst. I Regul. Pap. 65(2), 618–627 (2017) ArticleGoogle Scholar
- F. Cabello, J. León, Y. Iano, R. Arthur, Implementation of a fixed-point 2d Gaussian filter for image processing based on FPGA, in 2015 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA) (IEEE, 2015), pp. 28–33
- A. Chandra, S. Chattopadhyay, A new strategy of image denoising using multiplier-less fir filter designed with the aid of differential evolution algorithm. Multimed. Tools Appl. 75(2), 1079–1098 (2016) ArticleGoogle Scholar
- P.-Y. Chen, L.-D. Van, I.-H. Khoo, H.C. Reddy, C.-T. Lin, Power-efficient and cost-effective 2-d symmetry filter architectures. IEEE Trans. Circuits Syst. I Regul. Pap. 58(1), 112–125 (2010) ArticleMathSciNetGoogle Scholar
- P. Das, S.K. Naskar, S. Narayan Patra, Fast converging cuckoo search algorithm to design symmetric FIR filters. Int. J. Comput. Appl. 43(6), 547–565 (2021) Google Scholar
- A. Dehghani, A. Kavari, M. Kalbasi, K. RahimiZadeh, A new approach for design of an efficient FPGA-based reconfigurable convolver for image processing. J. Supercomput. 78(2), 2597–2615 (2022) ArticleGoogle Scholar
- F. Fons, M. Fons, E. Cantó, Run-time self-reconfigurable 2d convolver for adaptive image processing. Microelectron. J. 42(1), 204–217 (2011) ArticleGoogle Scholar
- K.K. Gundugonti, B. Narayanam, An area-power efficient denoising hardware architecture for real EOG signal. J. Circuits Syst. Comput. 29(15), 2050243 (2020) ArticleGoogle Scholar
- K.K. Gundugonti, B. Narayanam, Efficient Haar wavelet transform for detecting saccades and blinks in real-time EOG signal. SN Comput. Sci. 2(3), 1–7 (2021) ArticleGoogle Scholar
- K.K. Gundugonti, B. Narayanam, High speed fir filter using radix-2 r multiplier and its application for denoising EOG signal. J. Circuits Syst. Comput. 30(13), 2150237 (2021) ArticleGoogle Scholar
- N. Habibunnisha, D. Nedumaran, Hardware-based document image thresholding techniques using dsp builder and simulink, in Artificial Intelligence and Evolutionary Computations in Engineering Systems (Springer, 2022), pp. 207–220
- S. Kaur, M.S.M. Suman, S. Manna, Implementation of modified booth algorithm (radix 4) and its comparison with booth algorithm (radix-2). Adv. Electron. Electr. Eng. 3(6), 683–690 (2013) Google Scholar
- P. Kumar, P.C. Shrivastava, M. Tiwari, A. Dhawan, ASIC implementation of area-efficient, high-throughput 2-d IIR filter using distributed arithmetic. Circuits Syst. Signal Process. 37(7), 2934–2957 (2018) ArticleMathSciNetMATHGoogle Scholar
- P. Kumar, P.C. Shrivastava, M. Tiwari, G.R. Mishra, High-throughput, area-efficient architecture of 2-d block FIR filter using distributed arithmetic algorithm. Circuits Syst. Signal Process. 38(3), 1099–1113 (2019) ArticleGoogle Scholar
- V.K. Odugu, C. Venkata Narasimhulu, K. Satya Prasad, Design and implementation of low complexity circularly symmetric 2d FIR filter architectures. Multidimens. Syst. Signal Process. 31(4), 1385–1410 (2020) ArticleMATHGoogle Scholar
- V.K. Odugu, C. Venkata Narasimhulu, K. Satya Prasad, An efficient VLSI architecture of 2-d finite impulse response filter using enhanced approximate compressor circuits. Int. J. Circuit Theory Appl. 49(11), 3653–3668 (2021) ArticleGoogle Scholar
- A.K. Oudjida, N. Chaillet, Radix- \(2^r\) arithmetic for multiplication by a constant. IEEE Trans. Circuits Syst. II Express Briefs 61(5), 349–353 (2014) Google Scholar
- S. Palnitkar, Verilog HDL: A Guide to Digital Design and Synthesis, vol. 1 (Prentice Hall Professional, Hoboken, 2003) Google Scholar
- G. Rajakumar, A. Andrew Roobert, T. Arun Samuel, D. Gracia Nirmala Rani, Low power VLSI architecture design of BMC, BPSC and PC schemes. Analog Integr. Circuits Signal Process. 93(1), 169–178 (2017) ArticleGoogle Scholar
- P.-M. Seidel, L.D. McFearin, D.W. Matula, Secondary radix recodings for higher radix multipliers. IEEE Trans. Comput. 54(2), 111–123 (2005) ArticleGoogle Scholar
- O. Shipitko, A. Grigoryev, Gaussian filtering for fpga based image processing with high-level synthesis tools, in Proceedings of the IV International Conference on Information Technology and Nanotechnology, Sarma, Russia (2018), pp. 24–27
- V. Thamizharasan, N. Kasthuri, FPGA implementation of high performance digital FIR filter design using a hybrid adder and multiplier. Int. J. Electron. 1–21 (2022)
Author information
Authors and Affiliations
- Department of ECE, V R Siddhartha Engineering College, Vijayawada, 520007, India Gundugonti Kishore Kumar, Ravi Raja Akurati, Venkata Hanuma Prasad Reddy, Soumica Cheemalakonda, Sudeeksha Chagarlamudi, Bhasita Dasari & Sameera Sulthana Shaik
- Gundugonti Kishore Kumar

















